Question

Does y=3.5x +15 ever intersect with y=4x+10?And find that point.

Answer 1

Given that two lines are

y = 3.5x + 15

and y = 4x + 10

The condition for two lines to intersect is

`\begin{gathered} If\text{ a}_1x+b_1y+c_1=0\text{ and a}_2x+b_2y+c_2=0\text{ are two intersecting lines then } \\ it\text{ must satisfy }(a_1)/(a_2)\\e(b_1)/(b_2) \\ \end{gathered}`

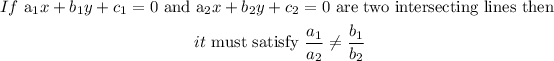
So, for the given lines the condition will be

`\begin{gathered} (3.5)/(4)\\e(15)/(10) \\ \end{gathered}`

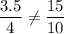
Since it had satisfied the condition then the given lines will intersect.

Now to find the intersecting point we will put both the equation equal.

3.5x + 15 = 4x + 10

4x - 3.5x = 15 - 10

0.5x = 5

x = 5/0.5 = 50/5

x = 10

So from the equation (i)

y = 3.5x + 15

y = 3.5 (10) + 15 = 35 + 15 = 50

y = 50

Hence the intersecting point is (x,y) = (10,50)