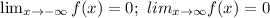Question

Question 13IT, pre calc, I am at work so please answer so I can review it later tonight, thanks

Answer 1

Step-by-step explanation

Dividing the numerator and denominator by the highest denominator power (x^2):

`=\lim _(x\to\: -\infty\: )\mleft(((1)/(x)+(1)/(x^2))/(1-(2)/(x))\mright)`

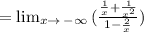
Applying the following property:

`\lim _(x\to a)\mleft[(f\left(x\right))/(g\left(x\right))\mright]=(\lim_(x\to a)f\left(x\right))/(\lim_(x\to a)g\left(x\right)),\: \quad \lim _(x\to a)g\mleft(x\mright)\\e0`

`With\: the\: exception\: of\: indeterminate\: form`

`=(\lim_(x\to\:-\infty\:)\left((1)/(x)+(1)/(x^2)\right))/(\lim_(x\to\:-\infty\:)\left(1-(2)/(x)\right))`

`=(\lim_(x\to\: -\infty\: )((1)/(x)+(1)/(x^2)))/(\lim_(x\to\: -\infty\: )(1-(2)/(x)))=(0)/(1)=0`

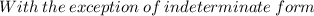
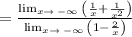
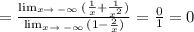
Now, we need to apply the same steps to x-> ∞

`\mathrm{Apply\: the\: following\: algebraic\: property}\colon\quad a+b=a\mleft(1+(b)/(a)\mright)`

`(x+1)/(x^2-2x)=(x\left(1+(1)/(x)\right))/(x^2\left(1-(2)/(x)\right))`

`=\lim _(x\to\infty\: )\mleft((x\left(1+(1)/(x)\right))/(x^2\left(1-(2)/(x)\right))\mright)`

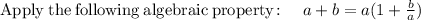
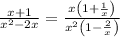
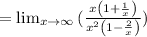
Simplifying:

`=\lim _(x\to\infty\: )\mleft((1+(1)/(x))/(-2+x)\mright)`

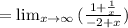
`\lim _(x\to a)\mleft[(f\left(x\right))/(g\left(x\right))\mright]=(\lim_(x\to a)f\left(x\right))/(\lim_(x\to a)g\left(x\right)),\: \quad \lim _(x\to a)g\mleft(x\mright)\\e0`

`\mathrm{With\: the\: exception\: of\: indeterminate\: form}`

`=(\lim_(x\to\infty\:)\left(1+(1)/(x)\right))/(\lim_(x\to\infty\:)\left(-2+x\right))`

`=(1)/(\infty\:)`

`\mathrm{Apply\: Infinity\: Property\colon}\: (c)/(\infty)=0`

`=0`

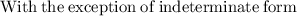
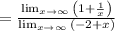
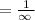
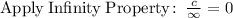
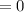
In conclusion, the appropiate end behavior is as follows:

`\lim _(x\to-\infty)f(x)=0;\text{ }lim_(x\to\infty)f(x)=0`