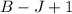Given:
Number of closed loops = L
Number of branches = B
Number of junctions = J
Let's determine the number of independent loop equation.
In a circuit, to write the equation which represents the number of independent loop, apply the Fundamental Theorem in Network Topology.
Since the circuit has L closed loops, B branches and J junctions, we have the equation:
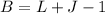
Now, for the number of independent loop rewrite the equation for L:
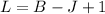
Therefore, the number if independent loop equation is:
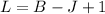
ANSWER: A