Step-by-step explanation
From the statement, we know that the speed of the cheetah is:
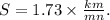
We have the following ratios:
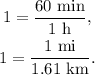
1) To convert the speed from km/min to mi/h, we rewrite the expression using the first ratio:
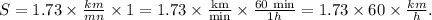
2) Now, we use the second ratio:
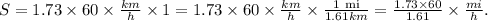
3) Finally, computing the product and quotient, we get:
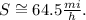
Answer
64.5 mi/h