Hello!
First, we have to find the radius of this circumference. We can obtain it using the formula to calculate the distance between two points, look:
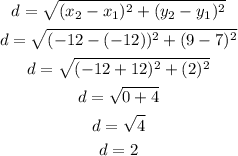
So, we know that:
• Center,: (-12, 7)
,
• Radius,: 2
To write the equation of the circle, we must use the formula below:
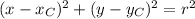
So, let's replace it with the values in the topics:
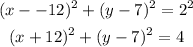
Look at it in the cartesian point below:
Answer:
(x+12)² + (y -7)² = 4