Answer
Explanation
Variables
• x: width of the rectangle, in ft
,
• y: length of the rectangle, in ft
Given that the length, y, is 30 feet less than 6 times the width, x, then:
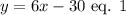
The area of a rectangle is calculated as follows:
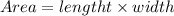
In this case, the area is 4836 square ft. Substituting this value and using the before defined variables, we get:
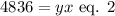
Substituting equation 1 into equation 2:
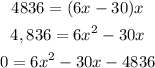
We can solve this equation with the help of the quadratic formula, as follows:
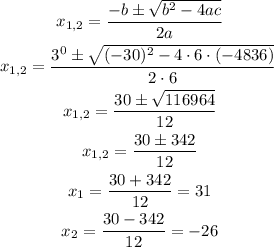
Given that the width cannot be negative, then the second solution is discarded.
Substituting x = 31 ft into equation 1: