Question

A pastry chef is making a batch of mini petit fours, which are little cakes, in the shape of cubes. To keep the nutritional value of each petit four consistent, the bakery manager wants each one to have a volume of 175cm^3. What should the side length be, to the nearest hundredth, for each petit four? (Note: for volume of a cube, v=s^3 where s= side length)

Answer 1

side length = 5.59 cm

Step-by-step explanation:

The volume V of a cube is given by

`V=s^3`

where s is the side length.

Now in our case, we are told that V = 175 cm^3; therefore, the above formula becomes

`175=s^3`

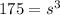
The problem is, we need the value of s. How do we extract it?

Well, we take the cube root of both sides of the above equation. This gives

`\sqrt[3]{175}=\sqrt[3]{s^3}`

The reason we did what we did above is that now the right-hand side simply becomes s and so the above equation gives

`\sqrt[3]{175}=s.`

Or more appropriately

`s=\sqrt[3]{175}`

Now to evaluate the above, we make use of a calculator and get

`\boxed{s=5.59.}`

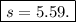
rounded to the nearest hundredth.

Hence, the side length of a cubic petit four is about 5.59 cm.