If two lines are perpendicular, then their slopes are opposite reciprocals.
This means that if you consider the lines:
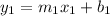
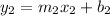
That are perpendicular, the relationship between their slopes is the following:
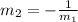
To determine the equation of a line perpendicular to y-2=4(x-1), the first step is to determine the value of its slope. This equation is given in the point-slope form which has the following structure:

Where
m represents the slope of the line
(x₁,y₁) represent the coordinates of one point of the line.
On the given equation, the slope is the coefficient that multiplies the parentheses term, m=4
We know that the slope of a line perpendicular to the given line will be the inverse opposite of m=4, then the slope of the perpendicular line will be:
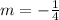
Using the coordinates of the given point (-4,5), the slope m=-1/4, and the point-slope form, you can determine the equation as follows:
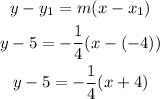
So, the equation of the line, that is perpendicular to y-2=4(x-1) and passes through the point (-4,5) is
