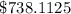Given that:
- The value of the computer when Robin bought it was $1,250.
- Its value will decrease by 10% each year that she owns it.
• You can identify that the first term of the sequence is:
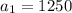
Knowing that it will depreciate by 10% each year, you can set up that the second term is (remember that a percent must be divided by 100 in order to write it in decimal form):
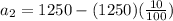
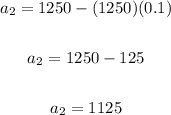
Notice that the third term is:
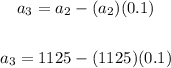
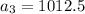
And the fourth term:
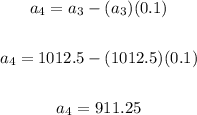
By definition, a term of a Geometric Sequence is obtained by multiplying the previous term by a constant called Common Ratio.
Therefore, you can check it this sequence is geometric as follows by identifying if there is a Common Ratio:
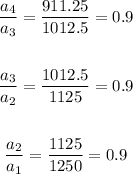
Notice that there is a Common Ratio:
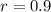
Therefore, it is a Geometric Sequence.
• By definition, the Explicit Formula of a Geometric Sequence has this form:
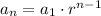
Where:
- The nth term is:
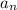
- The first term is:
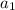
- The Common Ratio is:

- The term position is:
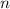
In this case, you already know the value of the first term and the Common Ratio. Therefore, you can substitute them into the formula in order to represent the sequence:
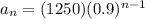
• In order to find the value of the computer at the beginning of the 6th year, you need to find the sixth term of the sequence:
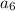
Therefore, you have to substitute this value of "n" into the Explicit Formula that represents the sequence and evaluate:
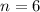
Then, you get:
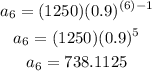
Hence, the answers are:
• It is a Geometric Sequence because it has a Common Ratio.
,
• Explicit Formula:
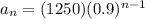
• Value of the computer at the beginning of the 6th year: