Question

Glven: AACZ and ACBZ are right triangles sin(A) sin(B) Prove: 8 a b Z B Statements Reasons AACZ and ACBZ are right triangles given -- multiplication property of equality bsin(A) = h, asin(B) = h bsin(A) = asin(B) transitive property of equality sin(A) sin(B) division property of equality What is the missing step of the proof? All rights reserved

Answer 1

Statement Problem: Given triangle ACZ and triangle CBZ are right triangles. What is the missing step in the prove;

`(\sin(A))/(a)=(\sin (B))/(b)`

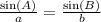
Solution:

Step 1: Given that triangle ABZ and triangle CBZ are right angles as shown in the diagram.

Step 2:

`\begin{gathered} \text{Recall that from trigonometry ratio for sine;} \\ \sin \theta=(opposite)/(hypotenuse) \\ \end{gathered}`

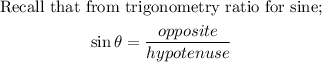
Hence, the missing statement is;

`\sin (A)=(h)/(b),\sin (B)=(h)/(a)`

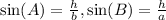
Reason:

The trigonometry ratio for sine