First, let's find the equivalent capacitance of the capacitors connected in series.
We can find it using the following formula:
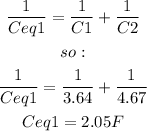
Now we can find the equivalent capacitance of the capacitors connected in parallel using the following formula:
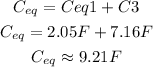
Answer:
9.21 F