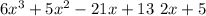
We start with 6x^3 divided by 2x
6x^3/2x = 3x^2
Multiply 3x^2 by (2x+5)
6x^3 + 15x^2
Now subtract the dividend by 6x^3 + 15x^2
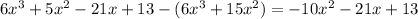
Divide the answer again by 2x
-10x^2/2x = -5x
Multiply -5x by (2x+5)
the answer is -10x^2 - 25 x
Subtract it from -10x^2 -21x + 13
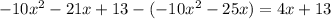
Divide 4x by 2x
4x/2x = 2
Multiply 2 by 2x+5
The answer is 4x + 10
Subtract it from 4x+13
4x+13 - (4x+ 10) = 3
So the quotient is
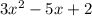
The remainder is 3
To check your answer multiply the quotient by the divisor
Let us do it
![undefined]()