Question

BP = _______ BC = ________ 13. AP = 3.5, PD = 6, PC = 4Find BP and BC.

Answer 1

Hello there. To solve this question, we have to remember some properties about circles and theorems relating chords.

Given the following diagram:

And the lengths of AP = 3.5, PD = 6 and PC = 4, we want to determine BP and BC.

Okay. First, we'll need the following theorem:

The theorem says that for the chords AC and BD, intersecting at E, it is true that

`AE\cdot EC=BE\cdot ED`

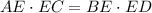
In this case, we have the lengths of three of the factors, therefore:

`BP\cdot PC=AP\cdot PD`

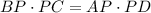
Plugging the values, we get

`BP\cdot4=3.5\cdot6`

Divide both sides of the equation by a factor of 4

`BP=3.5\cdot(6)/(4)=3.5\cdot1.5=5.25`

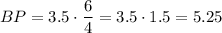
Finally, we know that

`BC=BP+PC`

Hence we get

`BC=5.25+4=9.25`

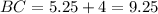
These are the answers to this question.