The given function is
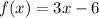
The domain is all the values of x that make the function defined
Since all real numbers make f(x) defined, then
The domain is all real numbers
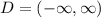
The range is all values of y corresponding to the domain
The range also is all real numbers
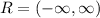
To find the zeroes equate f(x) by 0
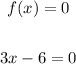
Add 6 to both sides
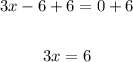
Divide both sides by 3
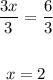
The zero of the function is (2, 0)
To draw the graph we will use 2 points
(2, 0) x-intercept
(0,-6) y-intercept
The red line is the graph of the given function