Given:
A plane flying a straight course observes a mountain at a bearing of 35° to the right of its course.
The distance between plan and mountain is 10 km.
A short time later, the bearing to the mountain becomes 45°.
Here NM is the distance between the plane from the mountain when the second bearing is taken.
We need to find the measure of NM.
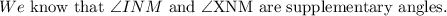
The sum of the supplementary angles is 180 degrees.
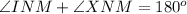

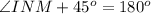
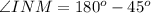

We know that the sum of all three angles of the triangle is 180 degrees.
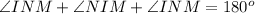
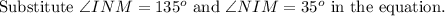
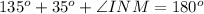
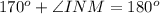
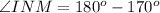
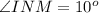
Consider the sine law.
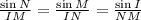
Take the equation to find the measure of NM.

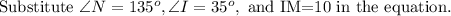

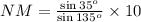
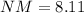
Hence the measure of NM is 8.1 km.
The plane is 8.1 km far from the mountain when the second bearing is taken.