Question

asked Nov 23, 2023 189k views

1 Answer

Ross Sheppard · Answer 1 · 2023-11-29T06:34:20+0000

Given:

A plane flying a straight course observes a mountain at a bearing of 35° to the right of its course.

The distance between plan and mountain is 10 km.

A short time later, the bearing to the mountain becomes 45°.

Here NM is the distance between the plane from the mountain when the second bearing is taken.

We need to find the measure of NM.

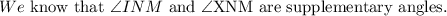
$We\text{ know that }\angle INM\text{ and }\angle\text{XNM are supplementary angles.}$

The sum of the supplementary angles is 180 degrees.

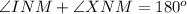
$\angle INM+\angle XNM=180^o$
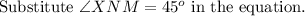
$\text{Substitute }\angle XNM=45^o\text{ in the equation.}$

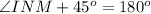
$\angle INM+45^o=180^o$

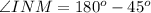
$\angle INM=180^o-45^o$

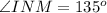
$\angle INM=135^o$

We know that the sum of all three angles of the triangle is 180 degrees.

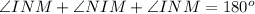
$\angle INM+\angle NIM+\angle INM=180^o$
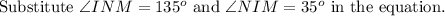
$\text{Substitute }\angle INM=135^o\text{ and }\angle NIM=35^o\text{ in the equation.}$

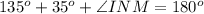
$135^o+35^o+\angle INM=180^o$

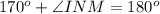
$170^o+\angle INM=180^o$

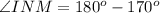
$\angle INM=180^o-170^o$

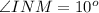
$\angle INM=10^o$

Consider the sine law.

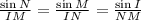
$(\sin N)/(IM)=(\sin M)/(IN)=(\sin I)/(NM)$

Take the equation to find the measure of NM.

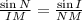
$(\sin N)/(IM)=(\sin I)/(NM)$
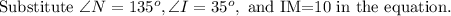
$\text{Substitute }\angle N=135^o,\angle I=35^o,\text{ and IM=10 in the equation.}$

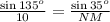
$(\sin 135^o)/(10)=(\sin35^o)/(NM)$

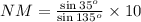
$NM=(\sin 35^o)/(\sin 135^o)*10$
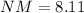
NM=8.11

Hence the measure of NM is 8.1 km.

The plane is 8.1 km far from the mountain when the second bearing is taken.

Please log in or register to add a comment.