Consider that the number of ways of selecting 'r' objects from 'n' distinct objects is given by,
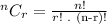
There are total 6 countries, out of which 4 is to be selected for the trip.
This means that 2 of the 6 countries have to be skipped.
So the number of ways of selecting 2 countries from 6 countries wull be,
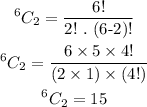
Thus, there are 15 ways to select 2 countries which are needed to be skipped.
Therefore, the second option is the correct choice.