Question

Use Pythagorean theorem to find the distance between McDonald's and sams clubReally need help it’s due in a few days

Answer 1

The figure has the following points

`\begin{gathered} \text{target T} \\ T(6,2) \\ \text{Mcdonald D} \\ D(1,4) \\ \text{Sam CLub S} \\ S(6,6) \end{gathered}`

In other to get the distance between McDonald's and Sam Club using Pythagoras theorem

Let the distance between Mcdonald and Sam Club be MS, it follows that

`\begin{gathered} MC^2=5^2+2^2 \\ MC^2=25+4 \\ MC^2=29 \\ MC=\sqrt[]{29} \\ MC=5.385 \end{gathered}`

a) Hence, the distance between Mcdonald's and Sam Club is 5.385

b) To get the distance between Mcdonald's and Target using the distance formula

The distance formula is given as

`\begin{gathered} A(x_1,y_1);B(x_2,y_2) \\ AB=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \end{gathered}`

`\begin{gathered} M(1,4) \\ T(6,6) \\ MT=\sqrt[]{(6-4)^2+(6-1)^2} \\ MT=\sqrt[]{2^2+5^2} \\ MT=\sqrt[]{4+25} \\ MT=\sqrt[]{29} \\ MT=5.385 \end{gathered}`

b) Hence, the distance between Mcdonald's and Target using the distance formula is 5.385

c) The midpoint formula is given as

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

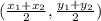
The midpoint of between McDonald's and Sam Club is

`\begin{gathered} M(1,4);S(6,6)^{} \\ \text{midpoint}=((6+1)/(2),(6+4)/(2)) \\ =((7)/(2),(10)/(2)) \\ =((7)/(2),5) \end{gathered}`

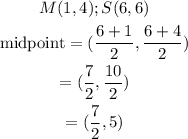
Hence, the midpoint between McDonald's and Sam Club is (7/2,5)