Answer:
• 4). The mean absolute deviation is 1.50 million (rounded to the nearest hundredth).
,
• 5). 8 data values
,
• 6). 8.4 million, 5.86 million
,
• 7)Yes, 8.4 million
Explanation:
Part 4
Given the data, first, we find the mean.
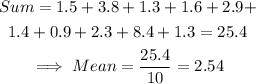
Next, subtract the mean from each of the data, take the absolute value and sum:

Therefore, the mean absolute deviation is:
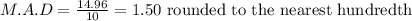
The mean absolute deviation is 1.50 million (rounded to the nearest hundredth).
Part 5
• The mean = 2.54 million
,
• The mean absolute deviation = 1.50 million
There are 8 data values that are closer than one mean absolute deviation away from the mean.
Part 6
The population that is farthest from the mean = 8.4 million
The distance away from the mean = |8.4-2.54| = 5.86 million.
Part 7
Twice the mean absolute deviation = 2 x 1.50 million = 3.00 million
Since 5.86 million > 3.00 million, the population of 8.4 million is greater than 3.00 million away from the mean.
Thus, the population 8.4 million is more than twice the mean absolute deviation from the mean.