Question

F(x)=x(x^3+1)+6x^2-8xhow many zeros does f have? explain how you know

Answer 1

Answer:

Four zeros

Explanations:

The given equation is given as:

`f(x)=x(x^3+1)+6x^2-8x`

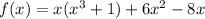
The function f(x) can be expanded to give:

`\begin{gathered} f(x)=x^4+x+6x^2-8x \\ f(x)=x^4+6x^2-7x \end{gathered}`

Note:

The zeros of a polynomial are the values of x that will make the function f(x) to be zero. This means that if those values (the zeros) are substituted into the function f(x), we will get 0 as the answer.

The number of zeros in a polynomial is the order of the polynomial

Therefore, the highest degree of the function f(x) above is 4, this means that the function f(x) has 4 zeros