We are given that a cyclist covers a distance of 20 km in 30 minutes. To determine the average speed we will use the following formula:
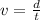
Where:
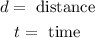
Since we desire to obtain the speed in units of km/h we need to convert the 30 minutes into hours. To do that we will use the following conversion factor:

Multiplying by the conversion factor we get:
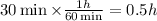
Now we substitute in the equation for speed:
![v=\frac{20\operatorname{km}}{0.5h}]()
Now we solve the operations:
![v=\frac{40\operatorname{km}}{h}]()
Part B. The average speed is 40 km/h. Since the average speed is the mean of the speed of the cyclist it is possible that a peak of 50 km/h could be reached.