Question

2. Consider the following points.A (-2 ,20) and P (10, -13) AP undergoes the translation Thk (x,y), such that A' (-28,37) and P' (-16,4). Part A: Complete the following algebraic description. (x,y)--->( x + , y+ )Part B Which of the following statements is true? A. AP and A'P' have different locations B. AP and A'P' have different shapesC. AP and A'P have different sizes.D. AP and A'P have different directions

Answer 1

We have a transformation applied to points A and P.

It is a translation, so we can write the generic rule as:

`(x,y)\longrightarrow(x+a,x+b)`

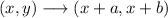
being a and b constants.

If A is (-2,20) and A' is (-28,37), we can find the values of a and b as:

`\begin{gathered} a=x^(\prime)-x=-28-(-2)=-26_{} \\ b=y^(\prime)-y=37-20=17 \end{gathered}`

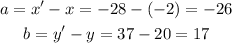
Then, the rule becomes:

`(x,y)\longrightarrow(x-26,y+17)`

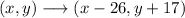
We will test it with P(10,-13):

`(10,-13)\longrightarrow(10-26,-13+17)=(-16,4)=P^(\prime)`

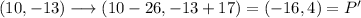
It gives P'(-16,4), so the rule is correct.

The segments AP and A'P' have the same length and orientation. The only difference is their location.

Answer:

(x,y)-->(x-26,y+17)

A. AP and A'P' have different locations.