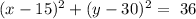Question

I need this problem from my prep guide answeredIt’s pre-calc

Answer 1

Question:

Solution:

The first step to solve this exercise is to find the center of the circle. According to the problem, the rectangle has vertices:

(0,0), (0,60), (30,60) and (30,0)

so they will form a rectangle with a width of 30 units and a height of 60 units.

Given this situation, the center of the rectangle is at (15,30), which is half of the width in the first coordinate and half of the height in the second one.

So that, the provisional equation of the flower garden will be:

`(x-15)^2+(y-30)^2=R^2`

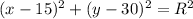
The final step is to find the value of R. That is, the value of the radius of the circle.

Given that the rectangular backyard width is 300 feet and this is represented with a rectangle in the blueprint with a width of 30 units, we get the following relationship:

`30unit\text{ = }300\text{ feet }\Rightarrow\text{ 60 f}eet\text{ }=((60)(30))/(300)\text{ units = 6 units}`

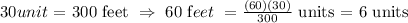
then, the radius of 60 feet is represented with 6 units in the blueprint. Now we replace R = 6 in the provisional equation of the circle:

`(x-15)^2+(y-30)^2=6^2\text{ = 36}`

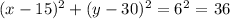
so that, we can conclude that the correct answer is:

`(x-15)^2+(y-30)^2=\text{ 36}`