Question

A person stands 30 meters east of an intersection and watches a car driving away from the intersection to the north at 17 meters per second. At a certain instant, the car is 16 meters from the intersection. What is the rate of change of the distance between the car and the person at that instant (in meters per second)?

Answer 1

8 meters per second

Explanation

To better understand the problem, we make the following sketch of the situation:

Let x be the distance between the car and the intersection (alonng AB)

Let y be the distance between the car and the person (along AC)

Let BC be 30 meters i.e. the distance between the person from the intersection.

The car is going away from the intersect at speed of 17 m/sec, therefore:

`(dx)/(dt)=17\text{ m/s}`

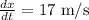
Now, by Pythagoras theorem on ABC:

`\begin{gathered} AC^2=AB^2+BC^2 \\ y^2=x^2+30^2\text{ (1)} \\ y=\sqrt[]{x^2+900}\text{ (2)} \end{gathered}`

Differentiate (1) with respect to t:

`\begin{gathered} 2y\cdot(dy)/(dt)=2x\cdot(dx)/(dt) \\ y\cdot(dy)/(dt)=x\cdot(dx)/(dt) \\ (dy)/(dt)=(x)/(y)(dx)/(dt) \end{gathered}`

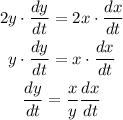
Replacing (2):

`(dy)/(dt)=\frac{x}{\sqrt[]{x^2+900}}(dx)/(dt)`

We evaluate when x is equal to 16, then:

`\begin{gathered} (dy)/(dt)=(16)/(√(16^2+900))\cdot17 \\ (dy)/(dt)=\frac{16}{\sqrt[]{256+900}}\cdot17 \\ (dy)/(dt)=\frac{16}{\sqrt[]{1156}}\cdot17 \\ (dy)/(dt)=(16)/(34)\cdot17 \\ (dy)/(dt)=8 \end{gathered}`

The rate of change of distance between the car and the person when the car is 16 m from the intersection is 8 m/sec