Question

Solve this system of equations byusing the elimination method.-3x + 8y = 43x – 2y = 8(1?-

Answer 1

`\begin{gathered} \text{Given} \\ -3x+8y=4 \\ 3x-2y=8 \end{gathered}`

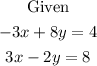
Add each terms from both equations

-3x + 8y = 4

+ (3x - 2y = 8)

0x + 6y = 12

6y = 12

Solve for y, using 6y = 12

`\begin{gathered} 6y=12 \\ (6y)/(6)=(12)/(6) \\ y=2 \end{gathered}`

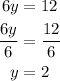
Substitute y = 2, to any of the two equation, in this case, we will use the second equation (using the first equation will yield the same result)

`\begin{gathered} \text{If }y=2,\text{ THEN} \\ 3x-2y=8\text{ \lparen second equation\rparen} \\ 3x-2(2)=8 \\ 3x-4=8 \\ 3x=8+4 \\ 3x=12 \\ (3x)/(3)=(12)/(3) \\ x=4 \end{gathered}`

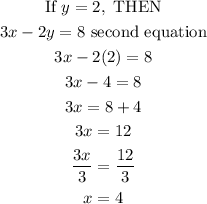
With x = 4, and y =2, the solution in ordered pair form is (4,2).