We need to find the rate of the current.
Let's call x the rate of the current. We know that the motorboat travels 12 mph in still water. Then, when it travels downstream, the current rate will be added to its velocity in still water.
Thus, in mph, its rate r₂ going downstream is:
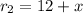
And, going upstream, it travels against the current. Thus, the current rate will be subtracted from its velocity in still water.
Thus, in mph, its rate r₁ going upstream is:
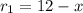
We know that the rate r of the motorboat is the distance traveled d divided by the time t during which it travels:
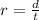
Thus, we have:
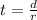
Now, for a distance d = 64 miles, the time t₁, in hours, to go upstream is one hour longer than the time t₂ to go downstream.
Thus, we have:
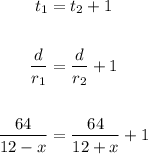
Then, rearranging the above equation, we obtain:
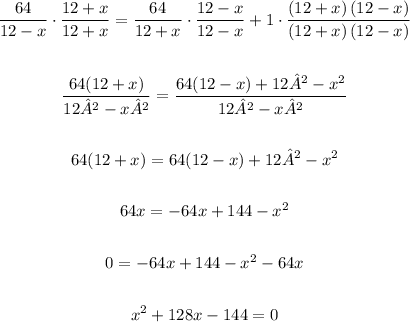
Now, solving the quadratic equation, we obtain:
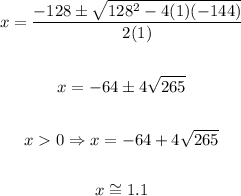
Therefore, the rate of the current is approximately 1.1 mph.