Question

The body temps of a group of healthy adults have a bell shaped distributions with a mean of 98.25F and a standard deviation of 0.68F. Using the empirical rule, find the approximate percentage below. 68% is the standard deviation. WHAT IS THE APPROXIMATE PERCENTAGE OF HEALTHY ADULT WITH BODY TEMPERATURE BETWEEN 96.89F AND 99.61F?

Answer 1

In the problem, the mean is:

`mean=98.25F`

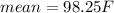
And the standard deviation:

`SD=0.68F`

We want to use the empirical rule to find which percentage of the data falls in the interval 96.89F - 99.61F

let's see how far from the mean are these values.

Let's add the standard deviation to the mean once:

`98.25+0.68=98.93F`

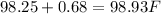
Let's add a standard deviation again:

`98.63+0.68=99.61F`

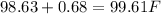
This is the right end of the interval. Is 2 standard deviations from the mean.

Let's do the same with the left end of the interval. If we subtract a standard deviation from the mean:

`98.25-0.68=97.57F`

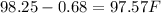
Once again:

`97.57-0.68=96.89F`

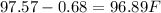
Thus, we just saw that the interval 96.89F-99.61F is the data that is within 2 standard deviation from the mean.

The empirical rule tell us that, in a normal data set 95% of the data is within 2 standard deviations from the mean.

Thus, the percentage of adults with temperatures between 96.89F and 99.61F is 95%