Question

A radio tower has a 33-foot shadow cast by the sun. If the angle from the tip of the shadow to the top of the tower is 77, what is the height of theradio tower Round your solution to four decimal places.

Answer 1

- To understand the question, let us sketch it out. This is done below:

- From the above illustration, we can see that the shadow and the tower make up part of a right-angled triangle with an adjacent of 33 feet and an angle of 77 degrees.

- Thus, to calculate the height of the tower, which is the Opposite of the triangle, we apply the tangent rule of triangles.

- The tangent rule is given below:

`\tan \theta=\frac{\text{Opposite }}{\text{Adjacent}}`

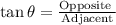
- With the formula above, we can proceed to solve the question as follows:

`\begin{gathered} \theta=77 \\ \text{Opposite}=\text{ Height}=\text{?} \\ \text{Adjacent}=33 \\ \\ \tan 77=\frac{Height}{\text{3}3} \\ \\ \text{ Height}=33*\tan 77 \\ \\ \therefore\text{Height}=142.938704\ldots\approx142.9387\text{ (To four decimal places)} \end{gathered}`

Final Answer

The Height of the tower is 142.9387 feet