We know that the function describing the amount remaining is given by:

In this case the initial amount is 20 and the decay rate is 0.02 in decimal form, hence the function we need is:

We want to know how long until the compound reaches one fourth of the original amount, this means that we need to find the time it takes to have 5 gr of the compond. Plugging this value in the function and solving for t we have:
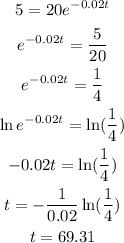
Therefore it takes approximately 69 years to have one forth of the orginal amount.