Question

Find the length of the bold arc. Round your answer to the nearest tenth.

Answer 1

The length of the bold arc is approximately 13.4 mi

Explanation:

The radius of the circle having the arc, r = 17 mi

Therefore, the circumference of the circle, 'C', is given as follows;

C = 2·π·r

∴ C = 2×π×17 = 34·π

The angle subtended by the arc = 45°

The sum of the angles at the center of the circle = 360°

By similarity, the ratio of the length of the bold arc to the circumference of the circle = The ratio of the angle subtended by the arc to the sum of the angles at the center of the circle

Mathematically, we have;

`(The \ arc \ length)/(C) = (\theta)/(360^(\circ))`

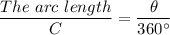
Therefore, we get;

`(The \ arc \ length)/(34 \cdot \pi) = (45 ^(\circ))/(360 ^(\circ)) = (1)/(8)`

`{The \ arc \ length}{} = (1)/(8) * 34 \cdot \pi = 4.25 \cdot \pi`

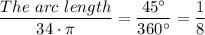
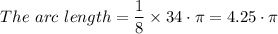
The length of the bold arc = 4.25·π mi ≈ 13.4 mi (by rounding off the answer to the nearest tenth).