We have the Newton's law of cooling:
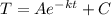
where:
A: initial difference of temperature between the object and the room temperature.
C: room temperature.
k: constant of cooling.
T: temperature of the object at time t.
We know that the initial temperature of the coffee is A+C = 174° and the room temperature is C = 73°.
Given a constant k = 0.0688919, we have to calculate the time t for which the coffe temperature T is 131°.
We can solve it as:
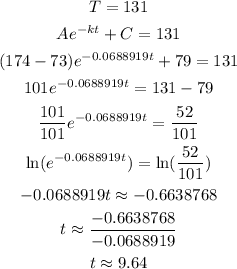
Answer: 9.64 minutes.