Question

Perform the indicated operation and express the result as a simplified complex number. (3−4i)(2+5i)

Answer 1

Given

`(3-4i)(2+5i)`

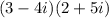
To solve the operation you have to distribute the multiplication, which means that you have to multiply each term of the first parentheses with each term of the second parentheses

`\begin{gathered} (3-4i)(2+5i) \\ (3\cdot2)+(3\cdot5i)-(4i\cdot2)-(4i\cdot5i) \\ 6+15i-8i-20i^2 \\ -20i^2+7i+6 \end{gathered}`

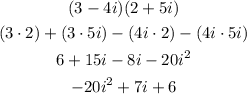
Now we know that the imaginary number "i" is equal to the square root of -1, so the square of i is equal to -1:

`\begin{gathered} i=\sqrt[]{-1} \\ i^2=(\sqrt[]{-1})^2 \\ i^2=-1 \end{gathered}`

Knowing this, we can simplify the result further:

`\begin{gathered} -20i^2+7i+6 \\ (-20)(-1)+7i+6 \\ 20+7i+6 \\ 20+6+7i \\ 26+7i \end{gathered}`

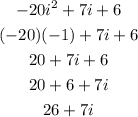
The result of the operation is 26 + 7i