Answer:
The time after which the two objects will collide is approximately 0.77 seconds
Step-by-step explanation:
Given that Object 1 and Object 2 start from a point relative to a common reference location, and have the following parameters;
The location Object 1 starts from = 5.4 m from the reference location
The velocity of Object 1, v₁ = 1.3 m/s
The location Object 2 starts from = 8.1 m from the reference location
The velocity of Object 2, v₂ = -2.2 m/s (the direction of the velocity is opposite to the direction of v₁)
Therefore, the distance between Object 1 and Object 2 when they start, 'd', is given as follows;
d = 8.1 m - 5.4 m = 2.7 m
At the time, 't', that elapse when the two objects collide, and given that the objects are moving in opposite direction, we have;
v₁·t - v₂·t = d
Plugging in the values of the variables, we get;
1.3 m/s × t - (-2.2 m/s) × t = 2.7 m
∴ t × (1.3 m/s + 2.2 m/s) = t × 3.5 m/s = 2.7 m
t = 2.7 m/(3.5 m/s) = (27/35) s =
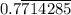 s ≈ 0.77 s
s ≈ 0.77 s
The time after which the two objects will collide, t ≈ 0.77 seconds.