Question

GRAPH each triangle and CLASSIFY the triangle according to its sides and angles.Number 2

Answer 1

GIVEN

A triangle DOG with the coordinates of the vertices given to be: D(1, 9), O(7, 9), and G(4, 2).

SOLUTION METHOD

To correctly classify the triangle, we need to get the lengths of each side of the triangle.

The formula to calculate the length of a line between two given points is given to be:

`AB=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Distance of Line DO:

`\begin{gathered} D=(x_1,y_1)=(1,9) \\ O=(x_2,y_2)=(7,9) \end{gathered}`

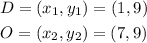
Therefore, the length is given to be:

`\begin{gathered} DO=\sqrt[]{(7-1)^2+(9-9)^2} \\ DO=\sqrt[]{6^2+0^2} \\ DO=\sqrt[]{36} \\ DO=6 \end{gathered}`

Distance of Line OG:

`\begin{gathered} O=(x_1,y_1)=(7,9) \\ G=(x_2,y_2)=(4,2) \end{gathered}`

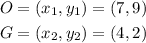
Therefore, the length is given to be:

`\begin{gathered} OG=\sqrt[]{(4-7)^2+(2-9)^2} \\ OG=\sqrt[]{(-3)^2+(-7)^2} \\ OG=\sqrt[]{9+49} \\ OG=\sqrt[]{58} \end{gathered}`

Distance of Line DG:

`\begin{gathered} D=(x_1,y_1)=(1,9) \\ G=(x_2,y_2)=(4,2) \end{gathered}`

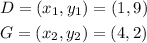
Therefore, the length is given to be:

`\begin{gathered} DG=\sqrt[]{(4-1)^2+(2-9)^2} \\ DG=\sqrt[]{3^2+(-7)^2} \\ DG=\sqrt[]{9+49} \\ DG=\sqrt[]{58} \end{gathered}`

The lengths of the sides are:

`\begin{gathered} DO=6 \\ OG=\sqrt[]{58} \\ DG=\sqrt[]{58} \end{gathered}`

CONCLUSION

Since two of the sides are equal, then the triangle is an ISOSCELES TRIANGLE.