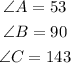Let me draw onto the given figure to better understand the problem.
Please refer to the figure below.
As you can see from the figure, angle A is equal to angle 53°.
They are called "Alternate Interior Angles" and they are always equal.
Similarly, angles 37° drawn in red color are also "Alternate Interior Angles".
Now we can find angle B.
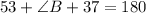
Angle B, angle 53°, and angle 37° form a "straight-line angle" that is 180°.
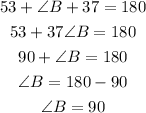
So the angle B is 90°
Now angle C and the sum of angle 53 and angle B are equal.
They are called "Vertically opposite angles" and they are always equal.
So we can write,
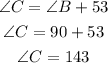
Therefore, the angles A, B, and C are