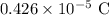Question

Two identical conducting spheres, fixed in place, attract each other with an electrostatic force of 0.162 N when their center-to-center separation is 59.6 cm. The spheres are then connected by a thin conducting wire. When the wire is removed, the spheres repel each other with an electrostatic force of 0.0482 N. Of the initial charges on the spheres, with a positive net charge, what was (a) the negative charge on one of them and (b) the positive charge on the other? (Assume the negative charge has smaller magnitude.)

Answer 1

Given data:

* The force of attraction between the charges is,

`F_a=-0.162\text{ N}`

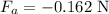
Here, the negative sign is indicating the attraction between the charges.

* The distance between the charges is,

`\begin{gathered} d=59.6\text{ cm} \\ d=0.596\text{ m} \end{gathered}`

* The force of repulsion between the charges is,

`F_r=0.0482\text{ N}`

Solution:

Let q_1 be the charge on the one sphere and q_2 is the charge on another sphere during the attraction.

According to Coulomb's law, the force of attraction between the charges in terms of the charges is,

`F_{}=(kq_1q_2)/(d^2)_{}`

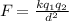
where k is the electrostatic force constant,

Substituting the known values,

`\begin{gathered} -0.162=(9*10^9* q_1q_2)/((0.596)^2) \\ q_1q_2=-(0.162*(0.596)^2)/(9*10^9) \\ q_1q_2=-0.0064*10^(-9) \\ q_1q_2=-0.64*10^(-11) \end{gathered}`

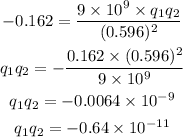
Thus, the charge q_2 in terms of the q_1 is,

`q_2=(-0.64*10^(-11))/(q_1)`

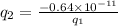
When the conductors are connected with the conducting wire, the charge distribution among both spheres takes place in such a way that both the spheres get the average of net charge (initial state).

The net charge in the initial state is,

`Q=(q_1+q_2)/(2)`

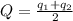
Thus, after the conducting wire, the charge on both the spheres is Q.

The electrostatic force between the sphere in the final state is,

`\begin{gathered} F_r=(kQ* Q)/(d^2) \\ 0.0482=(9*10^9*((q_1+q_2)/(2))^2)/((0.596)^2) \\ ((q_1+q_2)/(2))^2=(0.0482*(0.596)^2)/(9*10^9) \\ ((q_1+q_2)/(2))^2=0.0019*10^(-9) \end{gathered}`

By simplifying,

`\begin{gathered} ((q_1+q_2)/(2))^2=0.019*10^(-10) \\ (q_1+q_2)/(2)=0.138*10^(-5) \\ q_1+q_2=0.276*10^(-5) \end{gathered}`

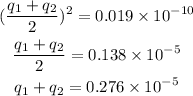
Substituting the known value of q_2,

`\begin{gathered} q_1-(0.64*10^(-11))/(q_1)=0.276*10^(-5) \\ q^2_1-0.64*10^(-11)=0.276*10^(-5)q_1 \\ q^2_1-0.276*10^(-5)q_1-0.64*10^(-11)=0 \end{gathered}`

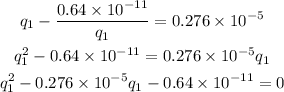
By solving the quadratic equation,

`\begin{gathered} q_1=\frac{0.276*10^(-5)\pm\sqrt[]{(0.276*10^(-5))^2-(4*(-0.64*10^(-11)))}}{2} \\ q_1=\frac{0.276*10^(-5)\pm\sqrt[]{0.076*10^(-10)+0.256*10^(-10)}}{2} \\ q_1=(0.276*10^(-5)\pm0.576*10^(-5))/(2) \\ q_1=0.426*10^(-5)\text{ C or -0.15}*10^(-5)\text{ C} \end{gathered}`

The value of charge q_2 is,

`\begin{gathered} q_2=-(0.64*10^(-11))/(0.426*10^(-5)) \\ q_2=-1.5*10^(-6)\text{ C} \\ q_2=-0.15*10^(-5)\text{ C} \end{gathered}`

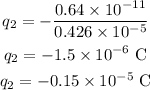
or

`\begin{gathered} q_2=-(0.64*10^(-11))/((-0.15*10^(-5))) \\ q_2=(0.64*10^(-11))/(0.15*10^(-5)) \\ q_2=4.26*10^(-6)\text{ C} \\ q_2=0.426*10^(-5)\text{ C} \end{gathered}`

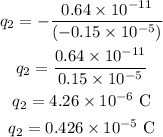
Thus, the possible combinations of the charges are,

`\begin{gathered} q_1=0.426*10^(-5)\text{ C} \\ q_2=-0.15*10^(-5)\text{ C} \\ or\text{ } \\ q_1=-0.15*10^(-5)\text{ C} \\ q_2=0.426*10^(-5)\text{ C} \end{gathered}`

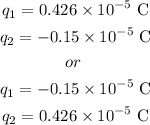
(a). Hence, the negative value of the charge is

`-0.15*10^(-5)\text{ C}`

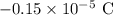
(b). Hence, the positive value of the charge is

`0.426*10^(-5)\text{ C}`