Question

A combined total of $55,000 is invested in two bonds that pay 2% and 7.5% simple interest. Theannual interest is $3,135.00. How much is invested in each bond?The amount invested at 2% is $IThe amount invested at 7.5% is $How you solve this ?

Answer 1

We are going to use the concept of simultaneous equations to answer this question;

x + y = $ 55000 .........................(1)

Recall that;

`\text{Interest = }(PRT)/(100)`
`\begin{gathered} \frac{x\text{ X 2 X 1}}{100}\text{ + }\frac{y\text{ X 7.5 X 1}}{100}\text{ = \$3135} \\ \\ (2x)/(100)\text{ + }(7.5y)/(100)\text{ = \$ 3135 (multiply through by 100)} \\ \\ 2x\text{ + 7.5y = \$313500 }\ldots\ldots\ldots\ldots\ldots.........(2) \end{gathered}`

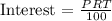
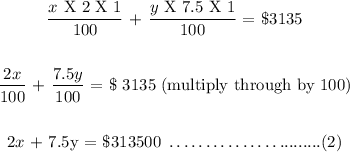
We can now solve the two equations simultaneously

From equation (1);

x = 55000 - y .............................(3)

Substitute equ.3 into equ. 2

2 (55000 - y) + 7.5y = 313,500

110,000 - 2y + 7.5y = 313,500

5.5y = 313,500 - 110,000

5.5y = 203,500 ( divide both sides by 5.5)

y = $37,000

Substitute y = 37,000 into equ 3

x = 55,000 - 37,000 = $18,000

Therefore, x = $18,000 and y = $37,000

The amount invested at 2% is $18,000 and the amount invested at the rate of 7.5% is $ 37,000