Question

A small college tracked its enrollment over a 5-year period and found the following results.Year Number of Students Enrolled11,55521,60231,65041,70051,751Which statement is true?O A. The enrollment can be modeled by an exponential function since the number of students is increasing by an approximately fixedpercentage each year.OB. The enrollment cannot be modeled by an exponential function since the number of students is not increasing by an approximatelyfixed percentage each year.OC. The enrollment can be modeled by an exponential function since the number of students is increasing by an approximately fixednumber of students each year.D. The enrollment cannot be modeled by an exponential function since the number of students is not increasing by an approximatelyfixed number of students each year.

Answer 1

We are given a set of data. We can determine how much of a percentage the number of students in the first year increases with respect to the second year using the following relationship:

`1555+1555*(n)/(100)=1602`

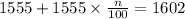
Where "n" is the percentage. WE solve for "n" first by subtracting 1555 to both sides:

`1555*(n)/(100)=1602-1555`

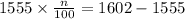
Now we divide both sides by 1555:

`(n)/(100)=(1602-1555)/(1555)`

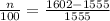
Now we multiply both sides by 100:

`n=(1602-1555)/(1555)*100`

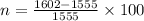
Solving the operations:

`\begin{gathered} n=(47)/(1555)*100 \\ n=0.003*100 \\ n=3 \end{gathered}`

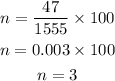
Therefore, we have a 3 percent increase. Now we check if this percentage is fixed for the other years.

`1602+1602*(3)/(100)=1602+48.06=1650`

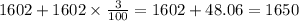
For year 4:

`1650+1650*(3)/(100)=1650+49.5=1699\approx1700`

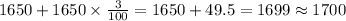
For the fifth year:

`1700+1700*(3)/(100)=1700+51=1751`

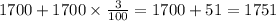
Therefore, each value increases by a fixed percentage of 3 per cent, therefore, the right answer is option B, since this means that the function can be modelled by an exponential function.