We have:
Total number of cards = 52
If you win then you will get = $70
If you lose then you will give him = $10
Therefore, first let us calculate the probability that three fives cards will be drawn with replacement:
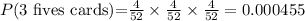
Next, the probability that it will not draw three fives in succession is:
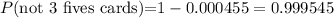
Hence, for each game the expected return would be:
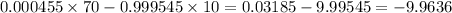
For 30 times:
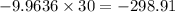
So, you lose $298.91
Answer:
Lose
$298.91