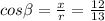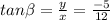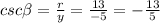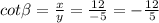Okay, here we have this:
Considering the provided angle, we are going to calculate the requested trigonometric functions, so we obtain the following:
So the first thing we will do is calculate the length of the hypotenuse, that is, the distance between the given point and the origin, then we have:
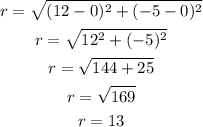
Now we proceed to find the value of each ratio: