Question

the longer leg of a right triangle is 7m longer than the shorter leg. the hypotenuse is 9m longer than the shorter leg find the side lengths of the triangle. length of the shorter leg:length of the longer leg:length of the hypotenuse:

Answer 1

Let "x" represent the shorter leg of the triangle.

Then, the long leg is 7m longer than the shorter leg, we can represent this as "x+7"

And the hypothenuse is 9m longer than the shorter leg, we can represent this as "x+9"

The Pythagoras theorem states that the square of the hypothenuse is equal to the sum of the squares of the sides of the triangle, so that:

`a^2+b^2=c^2`

a: shortest leg

b: longest leg

c: hypothenuse

Replace with the expressions for each side:

`x^2+(x+7)^2=(x+9)^2`

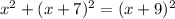
First solve both square of the binomials separatelly from the main expression:

1)

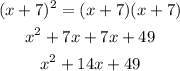
`\begin{gathered} (x+7)^2=(x+7)(x+7) \\ x^2+7x+7x+49 \\ x^2+14x+49 \end{gathered}`

2)

`\begin{gathered} (x+9)^2=(x+9)(x+9) \\ x^2+9x+9x+81 \\ x^2+18x+81 \end{gathered}`

Now that both terms are solved, input the results in the main expression

`\begin{gathered} x^2+(x+7)^2+(x+9)^2 \\ x^2+(x^2+14x+49)=(x^2+18x+81) \end{gathered}`

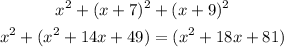
Now we need to equal the expression to zero, so perform the inverse operation to pass all terms to the left side of the equal sign

`\begin{gathered} x^2+(x^2+14x+49)-x^2-18x-81=x^2-x^2+18x-18x+81-81 \\ x^2+x^2+14x+49-x^2-18x-81=0 \end{gathered}`

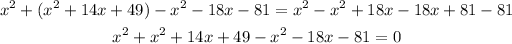
Order all like terms together and simplify:

`\begin{gathered} x^2+x^2-x^2+14x-18x+49-81=0 \\ x^2-4x-32=0 \end{gathered}`

With this, we stablished a quadratic expression. Using the quadratic formula we have to calculate the possible values of x

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

For our expression

a=1

b=-4

c=-32

Imput these values in the formula and calculate:

`\begin{gathered} x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4\cdot1\cdot(-4)}}{2\cdot1} \\ x=\frac{4\pm\sqrt[]{16+16}}{2} \\ x=\frac{4\pm\sqrt[]{32}}{2} \\ x=\frac{4\pm4\sqrt[]{2}}{2} \end{gathered}`

Now calculate both values of x:

Positive

`\begin{gathered} x=\frac{4+4\sqrt[]{2}}{2} \\ x=2+2\sqrt[]{2} \\ x\cong4.828 \end{gathered}`

Negative

`\begin{gathered} x=\frac{4-4\sqrt[]{2}}{2} \\ x=2-2\sqrt[]{2} \\ x\cong-0.828 \end{gathered}`

The length of the side of a triangle cannot be a negative value, so the only possible value of x will be:

`x=2+2\sqrt[]{2}=4.828m`

Now that we know the value of the shortest leg, we can calculate the value of the longest leg and the hypothenuse:

Longest leg

`x+7=(2+2\sqrt[]{2})+7=9+2\sqrt[]{2}\cong11.828m`

Hypothenuse

`x+9=(2+2\sqrt[]{2})+9=11+2\sqrt[]{2}\cong13.828m`