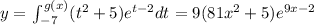Question

Use Part of the Fundamental Theorem of Calculus to find the derivative derivative of the function y

Answer 1

Find the derivative of the function:

`y=_{^{}}\int ^(9x)_(-7)(t^2+5)e^(t-2)dt_{}`

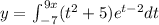
The Fundamental Theorem of Calculus I states that if f(x) is continuous over the interval [a,b] and the function F(x) is defined by:

`F(x)=\int ^x_af(t)dt`

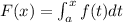
Then F'(x) = f(x) over [a,b]

We must find the derivative of y and the upper limit of the integral is not x, but a function of x: g(x) = 9x.

The only difference with the pure definition is that we have to use the chain rule for derivatives as follows:

`y=_{^{}}\int ^(g(x))_(-7)(t^2+5)e^(t-2)dt_{}=((9x)^2+5)e^(9x-2)\cdot g^(\prime)(x)`

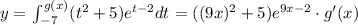
Since g'(x) = 9, then:

`y=_{^{}}\int ^(9x)_(-7)(t^2+5)e^(t-2)dt_{}=9((9x)^2+5)e^(9x-2)`

Operating:

`y=_{^{}}\int ^(g(x))_(-7)(t^2+5)e^(t-2)dt_{}=9(81x^2+5)e^(9x-2)`