Given:
The angle of incidence is,
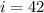
The refractive index of the crown glass for red light is,
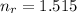
The refractive index of the crown glass for blue light is,
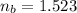
To find:
The angle separating rays of the two colours in a piece of crown glass
Step-by-step explanation:
We know, Snell's law,
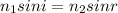
For, the red light,
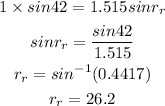
For, the blue light,
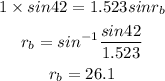
The separation between the refracted rays is,
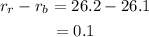
Hence, the required separation is 0.1 degrees.