To find the number of solutions of a system of linear equations you need to identify the slope (m) in each equation:

-If the slope is the same in both lines the system has no solution
-If the slope is different in the lines the system has one solution
-If the equation are the same (incluided the value of b) the system has infinitely many solutions
You have the next equations:

Write the equations in slope-intercept form y=mx+b (solve for y).
First equation:

Second equation:
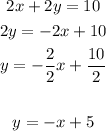
As the equations have the same slope m = -1, the system has no solution (the line doesn't cross each other)