Question

The center of a circle is located at (3, 5), and the radius is two units. The Pythagorean theorem can be applied to aninscribed right triangle to find the equation of the circle. What could be two of the vertices of the right triangle?

Answer 1

Given: The center of a circle is located at (3, 5), and the radius is two units.

Required: To use an inscribed right triangle to find the equation of the circle and vertices of the right triangle.

Step-by-step explanation: The following diagram can be drawn for the given information-

Let ABC be the right triangle inscribed in the circle with center O(3,5).

Let

`\begin{gathered} B=(x,y) \\ C=(p,q) \end{gathered}`

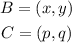
Now since OB and OC both are the radius of the circle. Hence we have

`OB=OC=2\text{ units}`

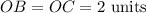
Hence we can write,

`3=(x+p)/(2);5=(y+q)/(2)`

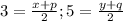
Solving the above equations we get