Question

Consider a watch with a diameter of 5.33 centimeters. a. What is the angular speed of the tip of the second hand? Include units in your answer. b. What is the tangential speed of the tip of the second hand? Include units in your answer. All answers must be in 3 significant digits.

Answer 1

Given data:

* The diameter of the watch is d = 5.33 cm.

* The radius of the watch is,

`\begin{gathered} r=(d)/(2) \\ r=(5.33)/(2) \\ r=2.66\text{ cm} \end{gathered}`

Solution:

(a). The second hand cover one complete oscillation on the watch in 60 seconds, thus, the linear frequency of the second hand is,

`f=(1)/(60)\text{ Hz}`

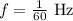
The angular frequency of the second hand is,

`\begin{gathered} \omega=2\pi f \\ \omega=2\pi*(1)/(60) \\ \omega=0.1047\text{ rad/s} \end{gathered}`

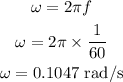
Thus, the angular speed of the tip is 0.1047 radians per second or 0.105 radians per second.

(b). The tangential speed of the second hand is,

`\begin{gathered} v=r\omega \\ v=2.66*0.1047 \\ v=0.278\text{ cm/s} \end{gathered}`

Thus, the tangential speed of the second hand is 0.278 cm/s.