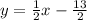Question

Determine the length of the line segment UV with U(3,-5) and V(-5,-9). Give your answer in simplified radical form. Find the equation of the line segment UV in Question 3

Answer 1

The length of the line segment will be calculated using the distance formula

The distance formula is given as

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

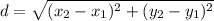
The line segment have the points U(3,-5) and V(-5,-9)

Therefoore the length of the line segment is:

`UV=√((-5-3)^2+(-9-(-5))^2)`

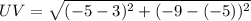
Calculate the value:

`\begin{gathered} UV=√((8)^2+(-4)^2) \\ UV=√(64+16) \\ UV=√(80) \\ UV=4√(5) \end{gathered}`

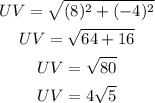
Therefore the length of the line segment is

`4√(5)`

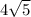
The equation of the line segment wil be determined using

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

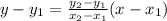
Therefore using the given points the equation of the line is:

`\begin{gathered} y-(-5)=(-9-(-5))/(-5-3)(x-3) \\ y+5=(-4)/(-8)(x-3) \\ y+5=(1)/(2)x-(3)/(2) \\ y=(1)/(2)x-(3)/(2)-5 \\ y=(1)/(2)x-(13)/(2) \end{gathered}`

Therefore the equation of the line segment is:

`y=(1)/(2)x-(13)/(2)`