Question

Point A has coordinates (5, -6) and point B has coordinates (7, 2).a)Find the coordinates of the midpoint of A and B.b)Find the gradient of the straight line AB.C)Find the equation of the straight line AB, giving the answer in the formy= mx + C.d)Find an equation of the perpendicular bisector of AB, giving the answer in theform ax+ by +C = 0, where a, b and care integers.

Answer 1

We have the coordinates of point A (5, -6) and point B has coordinates (7, 2).

Part A.

To find the coordinates of the midpoints

We will use the relationship

`(x_1+x_2)/(2),(y_1+y_2)/(2)`

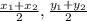
so that our midpoint will be

`\begin{gathered} (5+7)/(2),(-6+2)/(2) \\ (12)/(2),(-4)/(2) \\ \Rightarrow(6,-2) \end{gathered}`

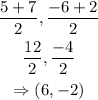
Part B

To find the gradient

`(y_2-y_1)/(x_2-x_1)=(2-(-6))/(7-5)=(8)/(2)=4`

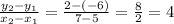
Gradient = 4.

Part C

The equation of the straight line AB, can be obtained as follow

`\begin{gathered} (y-y_1)/(x-x_1)=m \\ (y-(-6))/(x-5)=4 \\ \\ (y+6)/(x-5)=4 \end{gathered}`

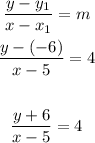
Cross multiply

`\begin{gathered} y+6=4(x-5) \\ y+6=4x-20 \\ y=4x-20-6 \\ y=4x-26 \end{gathered}`

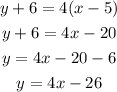
The equation of the straight line is: y= 4x -26

Part D

To get the equation of the perpendicular bisector, we will find the slope that is perpendicular to the line AB

since the slope of AB is 4

`\begin{gathered} \text{the slope perpendicular to the line will be} \\ m=-(1)/(4) \end{gathered}`

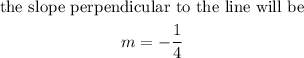
The midpoint is (6, -2)

Then the equation of the perpendicular bisector can be obtained as follow

`\begin{gathered} (y-(-2))/(x-6)=-(1)/(4) \\ \\ (y+2)/(x-6)=-(1)/(4) \end{gathered}`

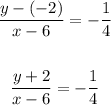
Cross multiply

`\begin{gathered} 4y+8=-x+6 \\ 4y+x+8-6=0 \\ 4y+x+2=0 \\ x+4y+2=0 \end{gathered}`

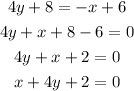
The equation of the perpendicular bisector is

x+4y+2=0