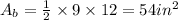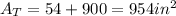Answer
• The lateral area of the prism is 900in².
,
• The total area of the prism is 954in².
Step-by-step explanation
The lateral area of a right triangle prism (AL) is given by:
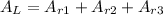
where Ar₁ represents the area of the first rectangle, Ar₂ the second, and Ar₃ the third. The area of a rectangle is given by:
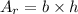
We have that b₁ = 12in, b₂ = 15in, and we don't know the value for b₃. However, we can calculate it with the Pythagorean Theorem:
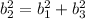
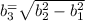
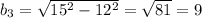
Then, the lateral area is the sum of Ar₁ , Ar₂, and Ar₃:


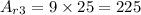
Thus, the lateral area is:
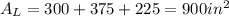
Finally, the total area (AT) is the addition of the area of the two bases (Ab) of the prism with the lateral area: