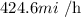Given
The plane horizontal altitude is 1 mi and speed is 450 mi/h.
The plane distance from the station is 3 mi.
Step-by-step explanation
Draw the figure,
P is the plane's position
R is the radar station's position
V is the point located vertically of the radar station at the plane's height.
h is the plane's height
d is the distance between the plane and the radar station
x is the distance between the plane and the V point
Since the plane flies horizontally, we can conclude that PVR is a right triangle. Therefore, the pythagoreas theorem is used to find x,
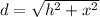
Substitute the values,
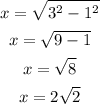
When d=3 mi, and, since the plane flies horizontally, we know that h=1mi regardless of the situation. We are looking for
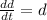
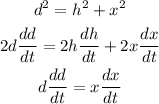
Substitute the values.
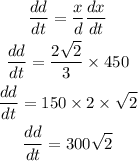
Answer
Hence the rate at which the distance from the plane to the station is increasing when it has a total distance of 3 mi away from the station is